오일러의 공식 (1) 멱급수, 매클로린 급수

오일러에 대해서 찾아보다가 멱급수를 연구하였다고 하기에 정리해보고자 합니다.

 

위키백과

저 빨간 박스 안의 식이 어떻게 유도되는지 보겠습니다.

 

---

멱급수

 

$ax^2+bx+c$

이 식은 많이 보던 다항식입니다.

이러한 다항식을

 

$a_{0}+a_{1}x+a_{2}x^2+a_{3}x^3+{...}$

이와 같이 다항식을 일반화 한 급수를 멱급수(power series)라고 합니다.

* 급수: 수열의 합

 

예를 들어,

$1+2x+3x^2+4x^3+{...}$

이 식은 멱급수입니다.

 

---

매클로린 급수

 

다음 함수를 생각해봅니다.

$f(x)=a_{0}+a_{1}x+a_{2}x^2+a_{3}x^3+{...}$

 

위 함수의 $x$에 0을 대입하면

$f(0)=a_{0}$

 

$f(x)$를 미분하면

$f'(x)=a_{1}+2a_{2}x+3a_{3}x^2+4a_{4}x^3+{...}$

 

위 함수의 $x$에 0을 대입하면

$f'(0)=a_{1}$

 

$f'(x)$를 미분하면

$f''(x)=2a_{2}+3\cdot 2a_{3}x+4\cdot 3a_{4}x^2+5\cdot 4a_{5}x^3+{...}$

 

위 함수의 $x$에 0을 대입하면

$f''(0)=2a_{2}$

즉

$a_{2}=\frac{f''(0)}{2}$

 

$f''(x)$를 미분하면

$f'''(x)=3\cdot 2a_{3}+4\cdot 3\cdot 2a_{4}x+5\cdot 4 \cdot 3a_{5}x^2+6\cdot 5\cdot 4a_{6}x^3+{...}$

 

위 함수의 $x$에 0을 대입하면

$f'''(0)=3\cdot 2a_{3}$

즉

$a_{3}=\frac{f'''(0)}{3\cdot 2}$

 

$a_{0}=f(0),\;a_{1}=f'(0),\;a_{2}=\frac{f''(0)}{2},\;a_{3}=\frac{f'''(0)}{3\cdot 2}$ 이므로

$a_{4}=\frac{f^{(4)}(0)}{4\cdot3\cdot2}$ 일 것이라 알 수 있습니다.

 

이것을 일반화시키면

$0!=1,\;1!=1$이므로

$a_{n}=\frac{f^{(n)}(0)}{n!}$입니다.

 

따라서 $f(x)$는 다음과 같은 전개식을 가질 수 있습니다.

 

$f(x)=\frac{f(0)}{0!}+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+{...}$

 

이 식을 $f$에 대한 매클로린 급수라고 합니다.

 

---

$\textrm{sin}x$을 매클로린 급수로 나타내기

 

$\textrm{sin}x$를 매클로린 급수로 나타내봅시다.

 

$f(x)=\frac{f(0)}{0!}+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+{...}$

 

$f(x)=\textrm{sin}x\quad\to \quad f(0)=0$

$f'(x)=\textrm{cos}x\quad\to \quad f'(0)=1$

$f''(x)=-\textrm{sin}x\quad\to \quad f''(0)=0$

$f'''(x)=-\textrm{cos}x\quad\to \quad f'''(0)=-1$

$f^{(4)}=\textrm{sin}x\quad\to \quad f^{(4)}(0)=0$

이므로

 

$\textrm{sin}x=\frac{0}{0!}+\frac{1}{1!}x+\frac{0}{2!}x^2+\frac{-1}{3!}x^3+\frac{0}{4!}x^4+\frac{1}{5!}x^5+\frac{0}{6!}x^6+\frac{-1}{7!}x^7+{...}$

 

즉

$\textrm{sin}x=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+{...}$

위 식으로 나타낼 수 있습니다.

 

 

그래프로 확인을 해보겠습니다.

(그래프를 그리는 프로그램은 옥타브(Octave)를 사용하였습니다.)

 

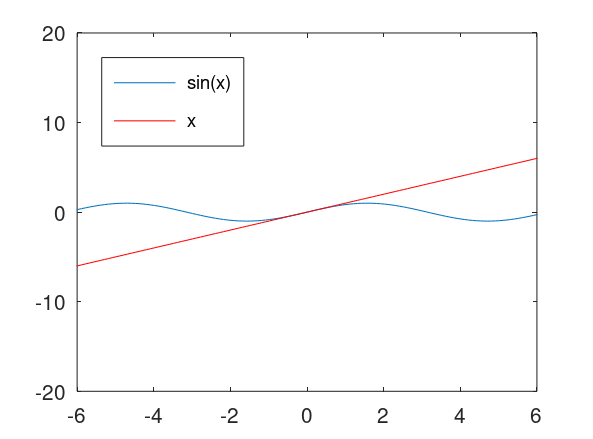
$f(x)=x$

 

x = [-2*pi:0.1:2*pi]
y = sin(x)
z1 = x
plot(x,y,x,z1,'r')
legend('sin(x)','x','Location','northwest')
axis([-6, 6, -20, 20])

 

 

 

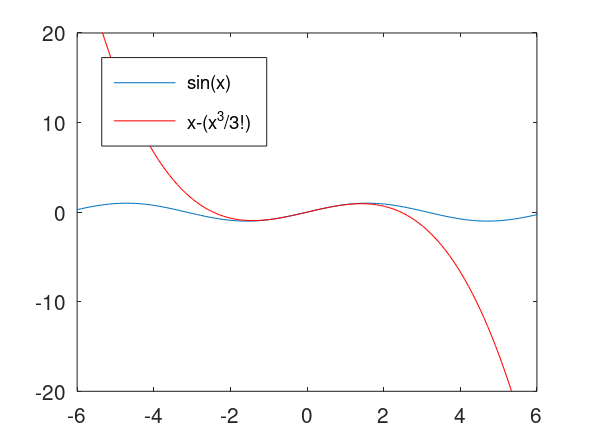
$f(x)=x-\frac{x^3}{3!}$

 

x = [-2*pi:0.1:2*pi]
y = sin(x)
z2 = x-x.^3./factorial(3)
plot(x,y,x,z2,'r')
legend('sin(x)','x-(x^3/3!)','Location','northwest')
axis([-6, 6, -20, 20])

 

 

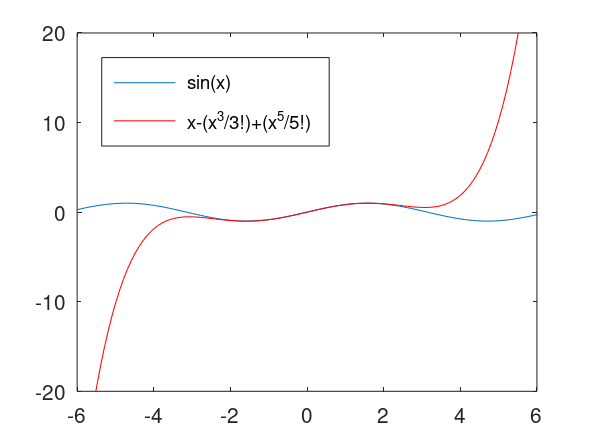
$f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}$

 

x = [-2*pi:0.1:2*pi]
y = sin(x)
z3 = x-x.^3./factorial(3)+x.^5./factorial(5)
plot(x,y,x,z3,'r')
legend('sin(x)','x-(x^3/3!)+(x^5/5!)','Location','northwest')
axis([-6, 6, -20, 20])

 

 

 

$f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}$

 

x = [-2*pi:0.1:2*pi]
y = sin(x)
z4 = x-x.^3./factorial(3)+x.^5./factorial(5)-x.^7./factorial(7)
plot(x,y,x,z2,'r')
legend('sin(x)','x-(x^3/3!)+(x^5/5!)-(x^7/7!)','Location','northwest')
axis([-6, 6, -20, 20])

 

 

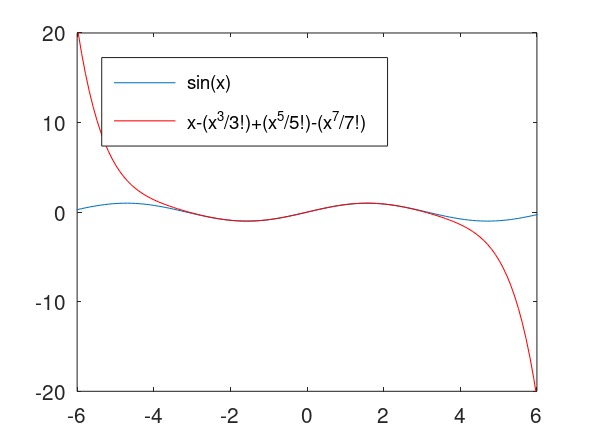
점점 $\textrm{sin}x$ 그래프에 가까워짐을 알 수가 있습니다.

 

x = [-2*pi:0.1:2*pi]
y = sin(x)
z1 = x
z2 = x-x.^3./factorial(3)
z3 = x-x.^3./factorial(3)+x.^5./factorial(5)
z4 = x-x.^3./factorial(3)+x.^5./factorial(5)-x.^7./factorial(7)
plot(x,y,x,z1,'r-',x,z2,'g--',x,z3,'m:',x,z4,'k-.')
legend('sin(x)','x','x-(x^3/3!)','x-(x^3/3!)+(x^5/5!)','x-(x^3/3!)+(x^5/5!)-(x^7/7!)','Location','northwest','NumColumns',2)
axis([-6, 6, -20, 20])

 

---

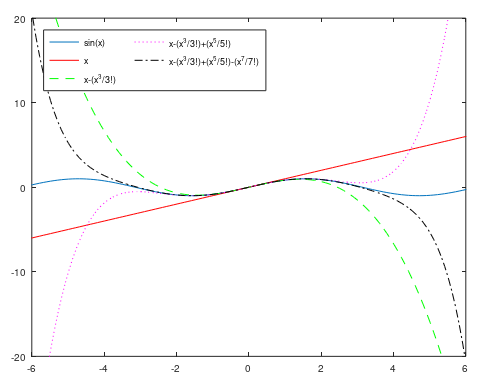
같은 방법으로 매클로린 급수로 

$\textrm{cos}x$와 $e^x$를 나타내면

 

$\textrm{cos}x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+{...}$

$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+{...}$

 

로 나타낼 수 있습니다.

 

 

다음 글에서는 위에서 설명한 수식들을 이용하여 '세상에서 가장 아름다운 수식'이라 불리는

 

$e^{i\pi}+1=0$

 

오일러 항등식을 유도해보겠습니다.